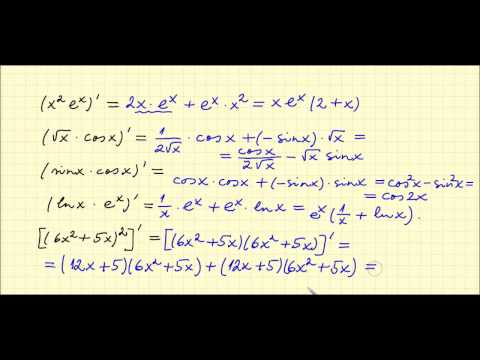
Sisu
Üks olulisi toiminguid, mida te arvutamisel teete, on tuletiste leidmine. Funktsiooni tuletist nimetatakse ka selle funktsiooni muutumise kiiruseks. Näiteks kui x (t) on auto asukoht igal ajal t, siis x tuletis, milleks on dx / dt, on auto kiirus. Samuti võib tuletise visualiseerida funktsiooni graafikule puutuja sirge kallakuna. Teoreetiliselt leiavad matemaatikud sellest tuletisi. Praktikas kasutavad matemaatikud põhireeglite komplekte ja otsingutabeleid.
Tuletis kallakuna
Kahe punkti vahelise joone kalle on y väärtuste tõus või erinevus y jagatuna käiguga või x väärtuste erinevus. Funktsiooni y (x) kalle x kindla väärtuse korral on määratletud selle funktsiooni puutuja sirge kallakuna. Kalde arvutamiseks konstrueeritakse joon punkti ja lähedal asuva punkti vahel, kus h on väga väike arv. Selle joone jaoks on käik või x väärtuse muutus h ja tõus või y väärtuse muutus on y (x + h) - y (x). Järelikult on y (x) kalle punktis ligikaudu võrdne / = / h. Kallaku täpseks saamiseks arvutage kalde väärtus, kui h muutub väiksemaks, kuni piirini, kus see nullitakse. Sel viisil arvutatud kalle on y (x) tuletis, mis kirjutatakse y '(x) või dy / dx.
Toitefunktsiooni tuletis
Funktsioonide tuletiste arvutamiseks, kus y võrdub x väärtusega a või y (x) = x ^ a, saab kasutada kalde / piiride meetodit. Näiteks kui y võrdub x kuubiga, y (x) = x ^ 3, siis dy / dx on piir, kui h läheb nulli / h. Laiendamine (x + h) ^ 3 annab / h, mis pärast h-ga jagamist väheneb 3x ^ 2 + 3xh ^ 2 + h ^ 2 -ni. Kui h läheb nulli, lähevad ka kõik terminid, milles neis h, nulli. Niisiis, y '(x) = dy / dx = 3x ^ 2. Saate seda teha muude väärtuste kui 3 korral ja üldiselt saate näidata, et d / dx (x ^ a) = (a - 1) x ^ (a-1).
Tuletis jõuseeriast
Paljusid funktsioone saab kirjutada nn energiaseeriana, mis on lõpmatu arvu terminite summa, kus igaüks on kujul C (n) x ^ n, kus x on muutuja, n on täisarv ja C ( n) on iga n väärtuse jaoks kindel arv. Näiteks siinusfunktsiooni toitesari on Sin (x) = x - x ^ 3/6 + x ^ 5/120 - x ^ 7/5040 + ..., kus “...” tähendab termineid, mis jätkuvad lõpmatuseni. Kui teate funktsiooni võimsuse seeriat, saate funktsiooni tuletise arvutamiseks kasutada võimsuse x ^ n tuletist. Näiteks Sin (x) tuletis on võrdne 1 - x ^ 2/2 + x ^ 4/24 - x ^ 6/720 + ..., mis juhtub olema Cosi (x) toitesari.
Tuletisinstrumendid tabelitest
Põhifunktsioonide, näiteks jõudude, näiteks x ^ a, eksponentsiaalsete funktsioonide, logifunktsioonide ja trigfunktsioonide tuletised leitakse kalde / piiride meetodi, võimsuse seeria meetodi või muude meetodite abil. Need tuletised loetletakse seejärel tabelites. Näiteks võite otsida, kas Sin (x) tuletis on Cos (x). Kui keerulised funktsioonid on põhifunktsioonide kombinatsioonid, vajate spetsiaalseid reegleid, näiteks ahelareeglit ja tootereeglit, mis on toodud ka tabelites. Näiteks kasutate ahelreeglit, et leida, et Sin (x ^ 2) tuletis on 2xCos (x ^ 2). Kasutate tootereeglit, et leida, et xSini (x) tuletis on xCos (x) + Sin (x). Tabelite ja lihtsate reeglite abil saate leida mis tahes funktsiooni tuletise. Kuid kui funktsioon on äärmiselt keeruline, pöörduvad teadlased mõnikord abi saamiseks arvutiprogrammide poole.