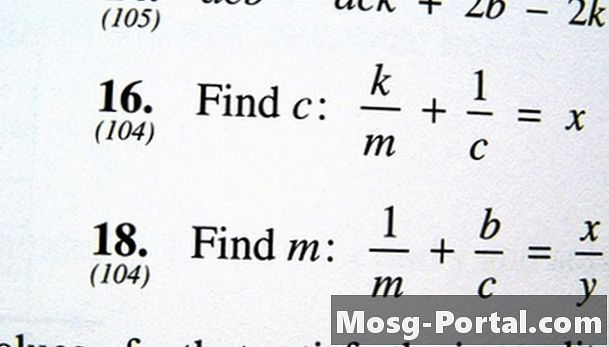
Monomaalid on üksikute arvude või muutujate rühmad, mis on ühendatud korrutisega. "X", "2 / 3Y", "5", "0,5XY" ja "4XY ^ 2" võivad kõik olla monomaalid, kuna üksikuid numbreid ja muutujaid ühendatakse ainult korrutamise teel. Seevastu "X + Y-1" on polünoom, kuna see koosneb kolmest monoomist, mis on ühendatud liitmise ja / või lahutamisega. Siiski saate monoomiale siiski lisada sellise polünoomi avaldise, kui need on sarnaste terminitega. See tähendab, et neil on sama muutuja sama eksponendiga, näiteks "X ^ 2 + 2X ^ 2". Kui monoom sisaldab murdosasid, siis liidaksite ja lahutaksite nagu tavalised terminid.
Pange paika võrrand, mida soovite lahendada. Kasutage näiteks võrrandit:
1 / 2X + 4/5 + 3 / 4X - 5 / 6X ^ 2 - X + 1 / 3X ^ 2 -1/10
Märge "^" tähendab "võimsusele", kusjuures number on eksponent või võimsus, millele muutujat tõstetakse.
Tuvastage sarnased terminid. Näites oleks kolm sarnast terminit: "X", "X ^ 2" ja muutujateta numbrid. Te ei saa erinevalt tingimustest lisada ega lahutada, seega võib teil olla lihtsam võrrandit rühmitamiseks sarnaste mõistetega ümber korraldada. Ärge unustage hoida liikuvate numbrite ees mingeid negatiivseid või positiivseid märke. Näites võite võrrandi korraldada järgmiselt:
(1 / 2X + 3 / 4X - X) + (4/5 - 1/10) + (-5 / 6X ^ 2 + 1 / 3X ^ 2)
Võite käsitleda igat rühma eraldi võrrandina, kuna te ei saa neid omavahel liita.
Leidke murdude jaoks ühised nimetajad. See tähendab, et iga liidetava või lahutatava murdosa alumine osa peab olema sama. Näites:
(1 / 2X + 3 / 4X - X) + (4/5 - 1/10) + (-5 / 6X ^ 2 + 1 / 3X ^ 2)
Esimeses osas on nimetajad vastavalt 2, 4 ja 1. "1" pole näidatud, kuid seda võib eeldada kui 1/1, mis ei muuda muutujat. Kuna nii 1 kui ka 2 lähevad ühtlaselt neljaks, võite kasutada ühiseks nimetajaks 4. Võrrandi korrigeerimiseks korrutate 1 / 2X 2/2 ja X 4/4-ga. Võite märgata, et mõlemal juhul korrutame me lihtsalt erineva murdosaga, mõlemad taanduvad väärtuseks "1", mis jällegi ei muuda võrrandit; see teisendab selle lihtsalt vormiks, mida saate kombineerida. Lõpptulemus oleks seega (2 / 4X + 3 / 4X - 4 / 4X).
Samuti oleks teisel osal ühine nimetaja 10, seega korrutaksite 4/5 2/2-ga, mis võrdub 8/10. Kolmandas rühmas oleks ühiseks nimetajaks 6, nii et saate korrutada 1 / 3X ^ 2 2/2-ga. Lõpptulemus on:
(2 / 4X + 3 / 4X - 4 / 4X) + (8/10 - 1/10) + (-5 / 6X ^ 2 + 3 / 6X ^ 2)
Liitmiseks lahutage lugejad või murdarvude ülaosa. Näites:
(2 / 4X + 3 / 4X - 4 / 4X) + (8/10 - 1/10) + (-5 / 6X ^ 2 + 3 / 6X ^ 2)
Oleks ühendatud järgmiselt:
1 / 4X + 7/10 + (-2 / 6X ^ 2)
või
1 / 4X + 7/10 - 2 / 6X ^ 2
Vähendage murdosa väikseima nimetajani. Näites on ainus arv, mida saab vähendada, -2 / 6X ^ 2. Kuna 2 läheb 6-ks kolm korda (ja mitte kuus korda), saab selle vähendada väärtuseks -1 / 3X ^ 2. Seetõttu on lõplik lahendus:
1 / 4X + 7/10 - 1 / 3X ^ 2
Kui laskuvad eksponendid teile meeldivad, saate neid uuesti ümber korraldada. Mõnele õpetajale meeldib selline korraldus, mis aitab vältida selliste terminite puudumist:
-1 / 3X ^ 2 + 1 / 4X + 7/10