Võrdkülgne kolmnurk on kolmnurk, mille kõik kolm külge on võrdse pikkusega. Kahemõõtmelise hulknurga, näiteks kolmnurga, pindala on polügooni külgede kogupindala. Ka võrdkülgse kolmnurga kolm nurka on Eukleidese geomeetrias võrdsed. Kuna Eukleidese kolmnurga nurkade kogupikkus on 180 kraadi, tähendab see, et kõik võrdkülgse kolmnurga nurgad on 60 kraadi. Võrdkülgse kolmnurga pindala võib arvutada, kui selle külje pikkus on teada.

Määrake kolmnurga pindala, kui alus ja kõrgus on teada. Võtke kaks identset kolmnurka aluse s ja kõrgusega h. Nende kahe kolmnurga abil saame alati moodustada aluse s ja kõrguse h rööpküliku. Kuna rööpküliku pindala on s x h, on kolmnurga pindala A seega ½ s x h.

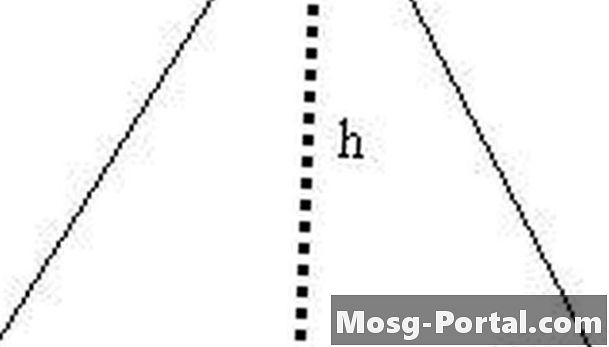
Vormige võrdkülgne kolmnurk sirgjoonega h kaheks parempoolseks kolmnurgaks. Nendest parempoolsetest kolmnurkadest ühe hüpotenuusi pikkus on s, ühel jalal on pikkus h ja teisel jalal pikkus s / 2.
Väljendage h s-ga. Kasutades 2. etapis moodustatud parempoolset kolmnurka, saame teada, et s ^ 2 = (s / 2) ^ 2 + h ^ 2 Pythagorase valemi järgi. Seetõttu on h ^ 2 = s ^ 2 - (s / 2) ^ 2 = s ^ 2 - s ^ 2/4 = 3s ^ 2/4 ja meil on nüüd h = (3 ^ 1/2) s / 2.
Asendage 3. etapis saadud h väärtus 1. etapis saadud kolmnurga pindala valemiga. Kuna A = ½ sxh ja h = (3 ^ 1/2) s / 2, on meil nüüd A = ½ s (3 ^ 1/2) s / 2 = (3 ^ 1/2) (s ^ 2) / 4.
Kasutage 4. etapis saadud võrdkülgse kolmnurga pindala valemit, et leida võrdkülgse kolmnurga pindala pikkusega 2. A = (3 ^ 1/2) (s ^ 2) / 4 = (3 ^ 1/2 ) (2 ^ 2) / 4 = (3 ^ 1/2).