Tasapinnalises geomeetrias võib ellipsi määratleda punktide kogumina, nii et nende kahe punkti (fookuse) vaheline summa on konstantne. Saadud joonist võib ka mittematemaatiliselt kirjeldada kui ovaalset või "lamestatud ringi". Ellipsidel on füüsikas mitmeid rakendusi ja need on eriti kasulikud planeetide orbiitide kirjeldamisel. Ekstsentrilisus on üks ellipsi omadustest ja see mõõdab ellipsi ümmargust kuju.
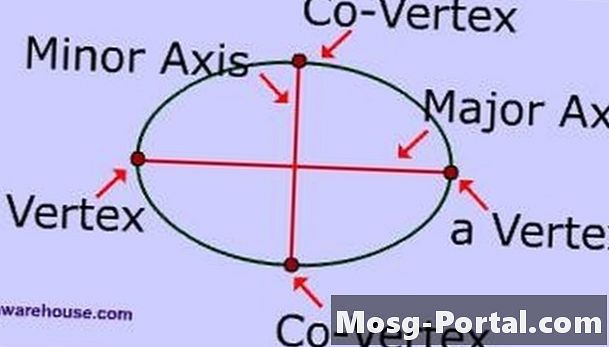
Uurige ellipsi osi. Suur telg on pikim sirgjoon, mis ristub ellipsi keskpunkti ja mille lõpp-punktid on ellipsil. Kõrvaltelg on lühim joone segment, mis ristub ellipsi keskpunkti ja mille lõpp-punktid on ellipsil. Peamine pooltelg on pool peateljest ja väiksem pooltelg on pool kõrvalteljest.
Uurige ellipsi valemit. Ellipsi matemaatiliseks kirjeldamiseks on palju erinevaid viise, kuid selle ekstsentrilisuse arvutamiseks ellipsi jaoks on kõige kasulikum järgmine: x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1. Konstandid a ja b on konkreetsele ellipsile omased ja muutujad on ellipsil paiknevate punktide x ja y koordinaadid. See võrrand kirjeldab ellipsi, mille keskpunkt on lähtepunktis ning põhi- ja kõrvalteljed, mis asuvad x- ja y-lähtepunktis.
Tehke kindlaks pooltelgede pikkused. Võrrandis x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1 on pooltelgede pikkused antud a ja b abil. Suurem väärtus tähistab peamist pooltelge ja väiksem väärtus väiksemat pooltelge.
Arvutage fookuste asukohad. Fookused asuvad põhiteljel, üks keskpunkti mõlemal küljel. Kuna ellipsi teljed asuvad lähtejoontel, on mõlema fookuse üks koordinaat 0. Teine koordinaat on (a ^ 2 - b ^ 2) ^ (1/2) ühe fookuse korral ja - (a ^ 2 - b ^ 2) ^ (1/2) teiste fookuste korral, kus a> b.
Arvutage ellipsi ekstsentrilisus suhtena fookuse kaugusest keskpunktist ja poolsuure telje pikkusest. Ekstsentrilisus e on seega (a ^ 2 - b ^ 2) ^ (1/2) / a. Pange tähele, et 0 <= e <1 kõigi ellipside korral. Ekstsentrilisus 0 tähendab, et ellips on ring ja pikal õhukesel ellipsil on ekstsentrilisus, mis läheneb 1-le.